In this article, we'll learn what is Surface Area, Formula for surface area of a cuboid and how to apply it.
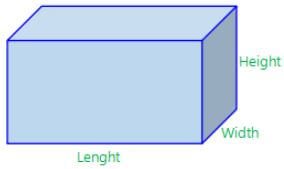
Surface area can be defined as the area of an outer part or the uppermost part of something. In case of a Cuboid, there are 6 rectangular surfaces, four walls, the top and the bottom surface. We label the dimensions of the cuboid with length(l), breadth (b) and the height(h).
Now the area of four walls is known as the Curved Surface Area or the Lateral surface Area of a Cuboid. The formula for Curved surface area of a cuboid is 2(l+b)h. Also the the area of four walls along with the top and bottom is known as Total surface area of a Cuboid. The formula to calculate the total surface area is 2(lb+bh+hl).
If you're wondering how these formulas have been derived, You can learn that with the below video.
Now, the area that we obtain for and geometrical shape is in square such square cm, sq. metres, sq. kms. Let's try to solve one problem based on surface area.
Example 1. The Dimensions of a cuboid are 10 cm length, 7 cm breadth and 5 cm height. Find the curved surface area and the total surface area of the cuboid.
Solution : L = 10 cm, b = 7 cm and h = 5cm
CSA of cuboid = 2(l+b)h = 2(10 + 7)5 = 2 * 17 * 5 = 170 cm²
TSA of cuboid = 2(lb + bh + hl) = 2[(10*7) + (7*5) + (5*10)] = 2[70 + 35 + 50] = 2 * 155 = 310 cm²
Example 2 : The Curved surface area of a cuboid is 96 cm². The length and breadth of the cuboid are 6 cm and 2 cm respectively. Find the height of the cuboid.
Solution: CSA = 96 cm² , l = 6 cm and b = 2 cm
CSA = 2(l + b)h -> 96 = 2(6 + 2)h -> 96 = 2*8*h -> 96 = 16h -> h = 96/16 -> h = 6 cm
Therefore, the height of the cuboid is 6 cm.
For more solved problems, you check out the below video:
If you want to learn the basic concepts of Arithmetic progression, Click on the link for the article.
I hope you like the article and learnt the concept of Surface area of Cuboid. Please share your feedback in the comments and don't forget to Subscribe Happy Learning for more videos.
No comments:
Post a Comment