Plays.org | Browser Based Ad free Gaming website

https://thehappylearning.in/?p=573

Plays.org Detailed article
@ thehappylearning.in

Video Review -
https://youtu.be/dZvbokefRC8

vacuum cleaner

Ecovacs Deebot 500 Robots Vacuum Cleaner Robotic Smart APP Control Max Mode Suction Power 3-Stage Cleaning System Compatible with Alexa

https://amzn.to/3jc6uZH

#HappyLearning

Kent Ro sale

https://amzn.to/3laT0iC

#Kent - 11076 New Grand 8-Litres Wall-Mountable RO + UV+ UF + TDS (White) 20 litre/hr Water Purifier

#waterpurifier #Amazon #affiliatedmarketing

one plus Nord Sale

https://amzn.to/2FJAMV5

One Plus Nord

INR 27999

Sale starts tomorrow at 1 PM

Don't miss the opportunity. Would love to know if you will be able to Add to Cart 🛒 & BUY 

How Elimination Method work

Elimination method is my second most favorite method to solve a pair of linear equations in two variables. In this article, we’ll understand the process of how to use Elimination method.

As discussed in the earlier article, we know the three methods to solve linear equations in two variables are Substitution Method, Elimination Method and Cross Multiplication Method. There are times when Elimination method will be most handy and will get the results faster then Substitution Method. Let’s dive right in, shall we?

You take one of the two equations and apply some transformation (that is multiply or divide the equation with some number) in order to make one of the x or y terms equal to the x or y term on second equation. Now that we have same x or y terms, subtract the resultant equation from equation number 2, in that way, on solving you’ll get the value of one variable (x or y). Then, put the value of variable you just got, into one of the original equations and solve for other variable. Now, you have the value of both the variables as the solution. Simple, isn’t it?

Let’s understand this method with one example. We have pair of linear equations –

2x + 3y = 8 —–> eq 1

x + 2y = 6 —–> eq 2

Please observe that if we multiply eq 2 with 2, we will have x term as 2x (equivalent to x term in eq 1). So, we multiply eq 2 with number 2, and we get

2x + 4y = 12 —–> eq 3

We mark it as eq 3. Now as have same x terms, we subtract equation 1(Minuend) from equation 3(subtrahend). While subtracting, we invert the sign of terms of equation being subtracted. So we have,

(2x + 4y = 12) – (2x + 3y = 8) => (y = 4)

Now we have y = 4. we put this value in eq 2 and solve it for x.

x + 2y = 6 => x + 2(4) = 6 => x + 8 = 6

=> x = 6 – 8 => x = – 2

Therefore, x = – 2, y = 4 is the solution to our given pair of linear equations.

I hope the method is clear to you. Still if you want to refer more solved examples. Check out Elimination Method video. You’ll find more videos on this Topic there on Happy Learning.

If you still have doubts, feel free to connect or leave your query in comments. Don’t forget to Subscribe Happy Learning for more videos. Thank you.

How Substitution Method works?

Substitution Method is the most easiest and straightforward technique to solve Linear equations in two variables. In this article, you'll learn how to use this method with the help of examples.

Linear equations in two variables is very important topics with examination point of view. There are three method with which we can solve the linear equations, namely, Substitution Method, Elimination Method and Cross Multiplication Method. You can definitely score good marks in examinations if you know how these techniques works.

As the name suggests, we have two variables in our linear equations and we marks both our equations as equation number 1 and equation number 2. We take one equation, say eq. no. 1 and express it in terms of x. Then we the expression equivalent to and substitute it in eq. no. 2. Now we solve this equation and obtain the value of y. Now that we have the value of variable y, we can again substitute value of y in the expression equivalent to x, to obtain the value of x. In this manner, we obtain the value of both the variables x and y. Simple, isn't it?

Just remember that the way we have expressed equation 1 in terms of x initially, you can express it in terms of y also and then proceed accordingly. Now let's take and example to understand how it works.

Let's say we have two equations :

x + y = 3 -------- eq 1
2x + 3y = 7 -------- eq 2

Now we take eq 1, and we express it in terms of x, and we'll have, x = 3 - y

We substitute the expression equivalent to x in eq 2, and we get,
2(3 - y) + 3y = 7
On solving we have, 6 - 2y + 3y = 7
Then, 6 + y = 7 => y = 7 - 6 = 1 => y = 1

Now we substitute value of y in expression equivalent to x,

x = 3 - y => x = 3 - 1 => x = 2

Therefore, solution to our linear equations is x = 2 and y = 1.

If you want to check more example refer this video Substitution Method

I hope you understood the concept. Don't forget to share your feedback and Subscribe Happy Learning. 

Surface Area Of A Cuboid

Cuboid

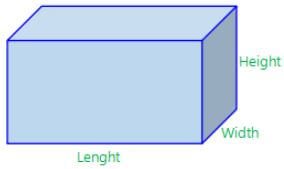
In this article, we'll learn what is Surface Area, Formula for surface area of a cuboid and how to apply it.

Surface area can be defined as the area of an outer part or the uppermost part of something. In case of a Cuboid, there are 6 rectangular surfaces, four walls, the top and the bottom surface. We label the dimensions of the cuboid with length(l), breadth (b) and the height(h).

Now the area of four walls is known as the Curved Surface Area or the Lateral surface Area of a Cuboid. The formula for Curved surface area of a cuboid is 2(l+b)h. Also the the area of four walls along with the top and bottom is known as Total surface area of a Cuboid. The formula to calculate the total surface area is 2(lb+bh+hl).

If you're wondering how these formulas have been derived, You can learn that with the below video.

How To Derive Formula for surface Area of Cuboid

Now, the area that we obtain for and geometrical shape is in square such square cm, sq. metres, sq. kms. Let's try to solve one problem based on surface area.

Example 1. The Dimensions of a cuboid are 10 cm length, 7 cm breadth and 5 cm height. Find the curved surface area and the total surface area of the cuboid.

Solution : L = 10 cm, b = 7 cm and h = 5cm

CSA of cuboid = 2(l+b)h = 2(10 + 7)5 = 2 * 17 * 5 = 170 cm²

TSA of cuboid = 2(lb + bh + hl) = 2[(10*7) + (7*5) + (5*10)] = 2[70 + 35 + 50] = 2 * 155 = 310 cm²

Example 2 : The Curved surface area of a cuboid is 96 cm². The length and breadth of the cuboid are 6 cm and 2 cm respectively. Find the height of the cuboid.

Solution: CSA = 96 cm² , l = 6 cm and b = 2 cm

CSA = 2(l + b)h -> 96 = 2(6 + 2)h -> 96 = 2*8*h -> 96 = 16h -> h = 96/16 -> h = 6 cm

Therefore, the height of the cuboid is 6 cm.

For more solved problems, you check out the below video:

If you want to learn the basic concepts of Arithmetic progression, Click on the link for the article.

I hope you like the article and learnt the concept of Surface area of Cuboid. Please share your feedback in the comments and don't forget to Subscribe Happy Learning for more videos.